Two sample proportion test calculator
The two proportion z test calculator with a step-by-step solution compares the proportions of two groups. We updated the calculator on 4-Dec-22 and changed the default continuity correction to don't use (false). (old calculator)
Two proportion z test calculator
Checks if the difference between the probability of succees (p) of two groups is significant, based on a sample data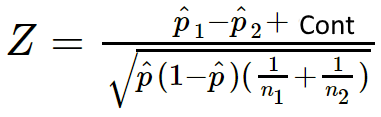
What is the continuity correction?
The continuity correction is applied when a continuous distribution is used to approximate a discrete distribution. In the two proportion z test, you use the continuous normal distribution to approximate the discrete binomial distribution.
Should I use the continuity correction?
By using the continuity correction, the results will be more similar to those obtained from the binomial distribution. However, in most cases the results with the normal approximation support a better results than the results with the binomial distribution, or the results with the continuity correction.
When using continuity correction
The continuity correction C adjust the statistic toward the zero.
p̂₁ < p̂₂: F = 1.
p̂₁ > p̂₂: F = -1.
p̂₁ = p̂₂: F = 0.
| C = | F | ( | 1 | + | 1 | ) |
| 2 | n1 | n2 |
The continuity correction cannot change the direction of the statistic i.e. correct positive statistic to negative, or vice versa.
C = Min(C, Abs(p1 - p2)).
| Z = | p̂₁ - p̂₂ + C |
| √( p̂(1-p̂)(1/n1 + 1/n2) ) |
Please note, the standard deviation in binomial distribution depends on the proportion. Since the null assumption of this test is that the proportions are equal, p1 = p2, when calculating the standard deviations we calculate it based on the pooled proportion:
| p̂*₁ = p̂*₂ = p̂ = | x₁ + x₂ |
| n₁ + n₂ |
Since the confidence interval doesn't assume that the proportions are equal, you can't reject the null assumption based on the confidence interval range.
Confidence interval statistics formula
When calculating the confidence interval of the difference between two proportions, we assume unequal proportions, p1 ≠ p2. Hence we calculate the standard deviation of each group based only on the individual group's data. In this caste we use p̂₁ and p̂₂ instead of p̂*₁ and p̂*₂.
| Z = | p̂₁ - p̂₂ |
| √(p̂₁(1-p̂₁)/n₁ + p̂₂(1-p̂₂)/n₂) |
Assumptions
- Independent samples - the samples were selected randomly and represent the populations.
- Binomial distribution - the probability for event within each group is identical
- Large sample size - The number of successes and failures in each sample should be large enough to use the normal approximation. As a rule of thumb, a sample size of at least 5 for both successes and failures is recommended.
Required Sample Data
- p̂₁, p̂₂ the sample probabilities or x1, x2 the number of successes
- n1, n2 - Sample size of group1 and group2