Two Sample Z-Test Calculator

Tests the expected difference between two populations' mean in the case that you know the population standard deviations.
The sample standard deviations are optional, and we only use them to validate the population standard deviations

or or enter summarized data (x̄, n, σ, S) below
*Not mandatory
When you enter raw data, the tool runs the Shapiro-Wilk normality test and calculates outliers.

Z-test claculator

Target: To check if the difference between the average (mean) of two groups is significant
Example1: A man of average height is expected to be 10cm taller than a woman of average height (d=10)
Example2: The average weight of an apple grown in field 1 is expected to be equal in weight to the average apple grown in field 2 (d=0)
Hypotheses
H0: μ1 = μ2+d
H1: μ1 ≠ μ2+d
Test statistic
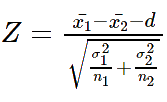
Z statistic
Normal distribution
z distribution two tailed

Assumptions

Normal DistributionNormal distribution
standard deviationσ1,σ2 - The standard deviations of both populations are known (either σ1=σ2 or ϭ1≠ϭ2 )

Required Sample Data

averagex1, x2 - Sample average of group1 and group2
sample sizen1,n2 - Sample size of group1 and group2



Examples
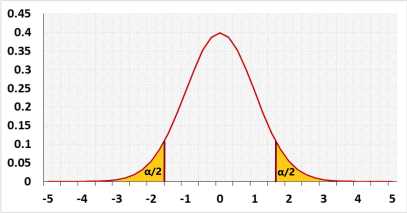
1. Two tailed test example:
A factory uses two identical machines to produce plastic plates. You would expect both machines to produce the same number of plates per minute.
We know the standard deviation of both machines.
Let μ1 = average number of plates produced by machine1 per minute.
Let μ2 = average number of plates produced by machine2 per minute.
We would expect μ1 to be equal to μ2. If one of the machines is slower than the other one, it should be serviced. In this case, we would like to know both if μ1 < μ2 or μ1 > μ2, since either machine could be slower.

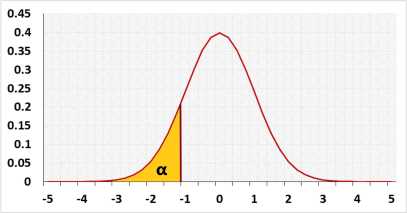
2. Left tail example.
A farmer uses fertilizer #1 with good results.
A friend told him fertilizer #2 is better than fertilizer #1.
Let μ1 = average number of potatoes per square meter in gardens using fertilizer #1.
Let μ2 = average number of potatoes per square meter in gardens using fertilizer #2.
The farmer assumes that the fertilizer currently in use (fertilizer #1) is better than the suggested one.(or equal)
He is willing to change fertilizer only if the new one is better.
The question of when to use the one-tailed test is controversial, some Statisticians claim that you should use the two tail even in this example, since it is still important to know that fertilizer #1 is better than fertilizer #2.