Kruskal Wallis Test Calculator
Followed by post-hoc Dunn's testData: use Enter or , (comma) or space as delimiters.
The tool ignores empty cells, non-numeric cells, or empty columns.
Kruskal Wallis Test
The Kruskal-Wallis test also called one-way ANOVA on ranks is a non-parametric test.Use the Kruskal-Wallis test calculator when your data doesn't meet the assumptions of the one-way ANOVA test calculator.
Target: To check if the difference between the ranks of two or more groups is significant, using a sample data
When the groups have a similar distribution shape, the null assumption is stronger and states that the medians of the groups are equal. When performing the Kruskal Wallis test, we try to determine, if the difference between the ranks reflects a significant difference between the groups, or is due to the random noise inside each group. The Chi-square statistic is an approximation for the exact calculation.
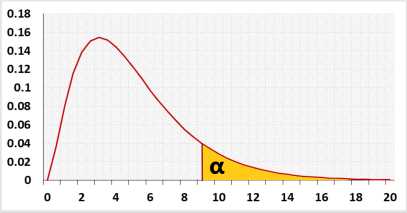
Right-tailed the Kruskal Wallis test can use only the right tail. Why?
| H'= | 12 | Σ( | Rj2 | ) - 3(n+1) |
| n(n+1) | nj |
| H= | H' |
| 1 - correction |
nj - the sample size of group j.
n - the total sample size across all groups, n = n1 +...+ nj.
Assumptions
- Independent samples from independent groups. One subject can't be in more than one group.
- The dependent variable is ordinal variable or continuous variable
- Two or more groups (the independent variable is categorical variable with two or more values)
Required Sample Data
- Sample data from all compared groups.
Multiple comparisons
Even if we know that not all the ranks are equal, we don't know which groups are not equal, hence we run a Multiple comparisons test to compare all the pairs.
We support two methods for the Multiple comparisons:
- Dunn's test calculator - takes into consideration the total number of groups (k) even when comparing only two groups
- Mann Whitney U test - the calculator uses the normal approximation of the Mann Whitney U test and supports the same results as the Kruskal Wallis test with two groups.